| Variable |
Description |
Units ( |
| Shear stress |
||
| Consistency index |
||
| Shear rate |
||
| Shear thinning index |
Unitless |
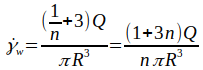
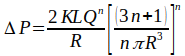
| Variable |
Description |
Units ( |
| Shear rate at the wall |
||
| Flow behaviour index (shear thinning index) |
Unitless |
|
| Volumetric flow rate |
||
| Radius of the cylinder |
||
| Pressure drop |
||
| Length of the flow path |
||
| Flow consistency index |
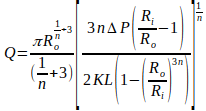
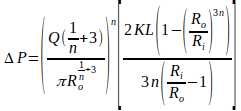
| Variable |
Description |
Units ( |
| Volumetric flow rate |
||
| Radius of the cone at the outled end |
||
| Radius of the cone at the inlet end |
||
| Flow behaviour index (shear thinning index) |
Unitless |
|
| Pressure drop |
||
| Length of the flow path |
||
| Flow consistency index |

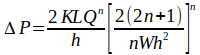
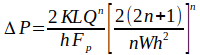
| Variable |
Description |
Units ( |
| Shear rate at the wall |
||
| Flow behaviour index (shear thinning index) |
Unitless |
|
| Width of the slot (major dimension of the
slot) |
||
| Height of the slot (minor dimension of the
slot) |
||
| Volumetric flow rate |
||
| Pressure drop |
||
| Length of the flow path |
||
| Flow consistency index |
||
| Correction factor for a narrow slot |
Unitless |
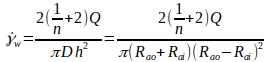

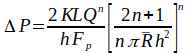
| Variable |
Description |
Units ( |
| Shear rate at the wall | ||
| Flow behavior index (shear thinning index) |
Unitless |
|
| Volumetric flow rate |
||
| Diameter of the center of the annulus (=(outer annulus diameter + inner annulus diameter)/2) |
||
| Height of the annulus (= (outer annulus
radius – inner annulus radius) |
||
| Outer annulus radius |
||
| Inner annulus radius |
||
| Radius of the center of the annulus (= (outer annulus radius + inner annulus radius)/2) |
||
| Pressure drop |
||
| Length of the flow path |
||
| Flow consistency index | ||
| Correction factor for a wide annulus |
Unitless |